1内容
example, in case $H$ has index two in $G$, for example in the case $G=S_{n}$ and $H=A_{n}$, then $G / H$ has order two and hence is 同构于 $\mathbb{Z} / 2 \mathbb{Z}$. But $S_{n}$ is not 阿贝尔群 if $n \geq 3$.
(iii) It is easy to see that, if $G$ is 循环的,那么$G / H$是循环的。例如,设 $G=\mathbb{Z} / n \mathbb{Z}$。那么对于每个 $d \mid n$,我们有子群 $H=\langle d\rangle$,阶为 $n / d$。由于 $G$是阿贝尔群,$H$自动成为 $G$的正规子群。因此 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle$是一个循环群,其阶等于 $\langle d\rangle$在 $\mathbb{Z} / n \mathbb{Z}$中的指数,即 $n /(n / d)=d$。因此 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$。(我们稍后将为此提供另一个证明。)
For future reference, we collect some facts about 正规子群. The 证明s are straightforward.
命题 2.3.14. Let $G$ be a 群 and let $H$ and $K$ be 子群 of $G$. Then:
(i) If $H \triangleleft G$ and $K \triangleleft G$,那么$H \cap K \triangleleft G$。
(ii) If $H \triangleleft G$ and $K \leq G$,那么$H \cap K \triangleleft K$。
(iii) If $H \leq K \leq G$ and $H \triangleleft G$,那么$H \triangleleft K$。
(iv) If $H \triangleleft G$ and $K \leq G$,那么子集
is a 子群 of $G$.
Remark 2.3.15. (i) Warning: It is possible that, in the above notation, we could have $H \triangleleft K$ and $K \triangleleft G$ but that $H$ is not a 正规子群 of $G$. In other words, the 性质 of being a 正规子群通常不具有传递性。习题 4.20中给出了示例。
(ii) If $H$ and $K$ are two arbitrary 子群 of $G$,neither one of which is 正规的,那么上述(4)中定义的$H K$不一定是子群。例如,取 $G=S_{3}, H=\langle(1,2)\rangle=\{1,(1,2)\}$ and $K=\langle(2,3)\rangle=\{1,(2,3)\}$,很容易看出
In particular, $\#(H K)=4$ and so $H K$ cannot be a 子群,since otherwise we would get a contradiction to 拉格朗日定理。
13. 正规子群与同态
3.1. 同态基本定理. We begin with a discussion of the relationship between 商群与同态。If $G$ is a 群 and $H \triangleleft G$,then we have the 商群 $G / H$ and the 商同态 $\pi: G \rightarrow G / H$,with 核 $\operatorname{Ker} \pi=H$。Conversely, suppose that $f: G_{1} \rightarrow G_{2}$ is a 同态 from a 群 $G_{1}$ to another 群 $G_{2}$。We want to analyze $f$ in terms of 商群。A first step is the following:
引理 3.1.1. If $f: G_{1} \rightarrow G_{2}$ is a 同态,那么核 $\operatorname{Ker} f$是$G_{1}$的正规子群。
证明. We must show that, for all $h \in \operatorname{Ker} f$ and for all $g \in G, g h g^{-1} \in \operatorname{Ker} f$,or equivalently that $f\left(g h g^{-1}\right)=1$。But, since $h \in \operatorname{Ker} f$,根据定义,$f(h)=1$,hence
Thus $\operatorname{Ker} f \triangleleft G_{1}$。
第一同构定理,also called the 同态基本定理,states among other things that every 同态 between two 群s is built up out of three basic types of 同态s: 商同态、同构和包含映射。
定理 3.1.2. Let $G_{1}$ and $G_{2}$ be 群s, let $f: G_{1} \rightarrow G_{2}$ be a 同态,and set $K=\operatorname{Ker} f \triangleleft G_{1}$ and $H=\operatorname{Im} f \leq G_{2}$。Then $G_{1} / K \cong H$。More precisely, if $\pi: G_{1} \rightarrow G_{1} / K$ is the 商同态 and if $i: H \rightarrow G_{2}$ is the 包含同态,then there is a unique 同构 $\tilde{f}: G_{1} / K \rightarrow H$ such that $f=i \circ \tilde{f} \circ \pi$。The situation is summarized by the following 图示:
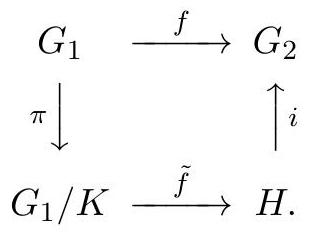
证明. We begin by trying to define the 函数 $\tilde{f}: G_{1} / K \rightarrow H$。Clearly, the only natural way to define $\tilde{f}$ on a 陪集 $g K$ is to set $\tilde{f}(g K)=f(g)$。In fact, this is also forced on us if we want $f=i \circ \tilde{f} \circ \pi$,because we must have $f(g)=i(\tilde{f}(\pi(g)))=i(\tilde{f}(g K))$,so $\tilde{f}(g K)=f(g)$。We must check that this is 良定义的,i.e. independent of the choice of 代表元 $g \in g K$。If instead we choose a different 代表元 of $g K$,necessarily of the form $g k$,then $f(g k)=f(g) f(k)=f(g) \cdot 1=f(g)$,hence $\tilde{f}$ is 良定义的,and its values $\tilde{f}(g K)=f(g)$ lie in $H=\operatorname{Im} f$。So we can view $\tilde{f}$ as a 函数 $G_{1} / K \rightarrow H$,and it is clearly 满射。Moreover, $\tilde{f}$ is a 同态 since
To see that it is an 同构,since we know that it is 满射,it suffices to show that it is 单射。Equivalently we must show that 核 $\operatorname{Ker} \tilde{f}=\{K\}$,the single element set consisting of the identity in $G_{1} / K$,namely the 单位陪集。Suppose that $\tilde{f}(g K)=1$。By definition $f(g)=\tilde{f}(g K)=1$,hence $g \in K$ and therefore $g K=K$。Thus 核 $\operatorname{Ker} \tilde{f}=\{K\}$ and hence $\tilde{f}$ is 单射,thus an 同构。(Compare also Remark 1.2.5.)
Finally we establish that $f=i \circ \tilde{f} \circ \pi$。To see that these two 函数 are equal, it is enough to check that they take the same value for every $g \in G$。But
where when we write $i(f(g))$ we view the term $f(g)$ as an element of $H=\operatorname{Im} f$ and in the final step of the equality we view $f(g)$ as an element of $G_{2}$。Thus $i \circ \tilde{f} \circ \pi(g)=f(g)$ for all $g \in G_{1}$,so that $f=i \circ \tilde{f} \circ \pi$。
推论 3.1.3. Let $G$ be a 群 and $H$ a 子群 of $G$。If there exists a 群 $G^{\prime}$ and a 满同态 $f: G \rightarrow G^{\prime}$ such that 核 $\operatorname{Ker} f=H$,then $H$ is a 正规子群 of $G$ and $G / H \cong G^{\prime}$。
We can sometimes use the 推论 to identify 商群 $G / H$ as more familiar 群s. The idea is to find a 同态 $f$ such that $H=\operatorname{Ker} f$。Here are some 示例:
例 3.1.4. (1) Let $G$ be a 群 and let $g \in G$。We have seen that there is a unique 同态 $f: \mathbb{Z} \rightarrow G$ such that $f(a)=g^{a}$ for all $a \in \mathbb{Z}$。Hence 像 $\operatorname{Im} f=\langle g\rangle$。If $g$ has 无限阶,then $f$ is 单射。If $g$ has 有限阶 $n$,then 核 $\operatorname{Ker} f=\langle n\rangle=n \mathbb{Z}$。Hence there is a unique 诱导同构 $\tilde{f}: \mathbb{Z} / n \mathbb{Z} \rightarrow G$ such that $\tilde{f}\left([a]_{n}\right)=g^{a}$ for all $a \in \mathbb{Z}$。
(2) The 同态 $f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(n, m)=n-m$ is 满射,and 核 $\operatorname{Ker} f= \{(n, n): n \in \mathbb{Z}\}=\langle(1,1)\rangle$。Hence $(\mathbb{Z} \times \mathbb{Z}) /\langle(1,1)\rangle \cong \mathbb{Z}$。More generally, if $\operatorname{gcd}(a, b)=1$,there is a 满同态 $\mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ with 核 $\langle(a, b)\rangle$,namely
Thus $(\mathbb{Z} \mathbb{Z}) /\langle(a, b)\rangle \cong \mathbb{Z}$ provided that $\operatorname{gcd}(a, b)=1$。
(3) We have seen that $f(t)=e^{i t}$ defines a 满同态 from $\mathbb{R}$(在加法下)到 $U(1)$ whose 核是 $\langle 2 \pi\rangle=2 \pi \mathbb{Z}$。Hence $\mathbb{R} / 2 \pi \mathbb{Z} \cong U(1)$ (a fact which also has 拓扑学意义)。Since multiplication by $2 \pi$ defines an 同构 from $\mathbb{R}$ to $\mathbb{R}$ such that the 像 of $\mathbb{Z}$ is $2 \pi \mathbb{Z}$,it follows easily that $\mathbb{R} / \mathbb{Z}$ is also 同构 to $U(1)$。In fact, the 同态 $g(t)=e^{2 \pi i t}$ has 核 $\mathbb{Z}$ and 像 $U(1)$,and thus $\mathbb{R} / \mathbb{Z} \cong U(1)$ as well。Using this 同构,we see that the 挠子群 of $U(1)$,which by definition is $\mu_{\infty}$,is 同构 to $\mathbb{Q} / \mathbb{Z}$。
(4) Let $G_{1}$ and $G_{2}$ be two 群s, with 正规子群 $H_{1} \triangleleft G_{1}$ and $H_{2} \triangleleft G_{2}$,and let $\pi_{1}: G_{1} \rightarrow G_{1} / H_{1}$ and $\pi_{2}: G_{2} \rightarrow G_{2} / H_{2}$ be the 商同态。Then there is a 同态
defined by $\pi\left(g_{1}, g_{2}\right)=\left(\pi_{1}\left(g_{1}\right), \pi_{2}\left(g_{2}\right)\right)=\left(g_{1} H_{1}, g_{2} H_{2}\right)$。Clearly $\pi$ is 满射 and 核 $\operatorname{Ker} \pi= H_{1} \times H_{2}$。Thus
In particular, taking $H_{1}=\{1\}$ and $H_{2}=G_{2}$ shows that
For example, taking $G_{1}=G_{2}=\mathbb{Z}$,we see that $(\mathbb{Z} \times \mathbb{Z}) /(\{0\} \times \mathbb{Z}) \cong \mathbb{Z}$,where $\{0\} \times \mathbb{Z}= \langle(0,1)\rangle$。Similarly, if $W$ is a 向量子空间 of the 有限维向量空间 $V$,say $\operatorname{dim} V=n$ and $\operatorname{dim} W=d$,then there is a 基 $e_{1}, \ldots, e_{n}$ of $V$ such that $W= \operatorname{span}\left\{e_{1}, \ldots, e_{d}\right\}$。This identifies $V$ with $\mathbb{R}^{n}$ and $W$ with the 向量子空间 $\mathbb{R}^{d}$ consisting of all vectors whose last $n-d$ coordinates are zero。Hence $V \cong \mathbb{R}^{n} \cong \mathbb{R}^{d} \times \mathbb{R}^{n-d}$,in such a way that the 子空间 $W$ is identified with the first factor $\mathbb{R}^{d}$,so that the 商空间 $V / W \cong \mathbb{R}^{n-d}$。Here, $V / W$ is more than just a 群,since $W$ is more than just a 子群 of $V$ (it is in addition closed under 标量乘法),and in fact $V / W$ is a 向量空间 in its own right。
3.2. 第二同构定理与第三同构定理. One reason to call $G / H$ a 商群 is that the notation $G / H$ has many properties that look like the analogous ones for 分数。For example, $G / G \cong\{1\}$ and $G /\{1\} \cong G$。We have also seen that, for $H_{1} \triangleleft G_{1}$ and $H_{2} \triangleleft G_{2},\left(G_{1} \times\right. \left.G_{2}\right) /\left(H_{1} \times H_{2}\right) \cong\left(G_{1} / H_{1}\right) \times\left(G_{2} / H_{2}\right)$。Another property is the following: We called 定理 3.1.2 the 第一同构定理,so we naturally expect there to be other 同构定理s as well。We shall first state and 证明 the 第三同构定理:
定理 3.2.1. Let $G$ be a 群 and let $H$ and $K$ be 正规子群 of $G$ with $H \leq K$。Let $\pi: G \rightarrow G / H$ be the 商同态。Then $K / H=\pi(K)$ is a 正规子群 of $G / H$,and
(The way to remember this is that, if we think the expressions $G / H, K / H$ as 分数,then the denominators above cancel each other.)
证明. We will 证明 the 定理 by applying the 第一同构定理。Begin by defining $f: G / H \rightarrow G / K$ by: $f(g H)=g K$。Here $f$ is a 函数 defined on the set of 陪集 $G / H$ by choosing a 代表元,so we must check that $f$ is 良定义的。If $g^{\prime} \in g H$ is another 代表元,then $g^{\prime}=g h$ for some $h \in H$ and so $g^{\prime} K=g h K=g K$,since $g h$ and $g$ differ by an element of $H$ and hence of $K$ since $H \subseteq K$。Clearly $f$ is 满射。Also,
Hence $f$ is a 同态。Finally,
Hence $K / H \triangleleft G / H$ and $(G / H) /(K / H) \cong G / K$ by the 第一同构定理。
Remark 3.2.2. An equivalent formulation is the following: Suppose that $f: G \rightarrow G^{\prime}$ is a 满同态 and that $N^{\prime}$ is a 正规子群 of $G^{\prime}$。Then $f^{-1}\left(N^{\prime}\right)=N$ is a 正规子群 of $G$ and the 复合同态 $G \rightarrow G^{\prime} / N^{\prime}$ is a 满射 with 核 $N$。Hence, by the 第一同构定理,$G / N \cong G^{\prime} / N^{\prime}$。
例 3.2.3. Suppose that $n, d \in \mathbb{N}$ and that $d \mid n$。Then $\langle n\rangle \leq\langle d\rangle \leq \mathbb{Z}$,and all 子群 of $\mathbb{Z}$ are 正规的 since $\mathbb{Z}$是阿贝尔群。The 像 of $\langle d\rangle$ in $\mathbb{Z} /\langle n\rangle=\mathbb{Z} / n \mathbb{Z}$ is the 循环子群 generated by $d$ viewed as an element of $\mathbb{Z} / n \mathbb{Z}$。Applying the 第三同构定理,we see that $\mathbb{Z} / n \mathbb{Z} /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$,which we have also argued by a direct inspection of the 陪集 and the 群运算。
To describe the 第二同构定理,we recall from 习题 4.25 that, if $H$ and $K$ are two 子群 of $G$,with $H \triangleleft G$,then $H K$ is a 子群 of $G, H \triangleleft H K$ and $H \cap K \triangleleft K$。Thus, we can consider the 商群 $H K / H$。The 第二同构定理 gives another description of this 商:
定理 3.2.4. Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Then
In particular, if $H$ and $K$ are both 有限的,then
证明. By 习题 4.25,$H \cap K \triangleleft K$ (although we will see this directly as well),$H K \leq G$ and $H \triangleleft H K$。
To prove the 定理,we shall find a 满同态 $f$ from $K$ to $H K / H$ whose 核是 $H \cap K$。The 第一同构定理 then says that $K /(H \cap K) \cong H K / H$。Define $f(k)=k H$,包含$k$的$H$-陪集。Thus $f$ is the 复合映射 $\pi \circ i$,where $i: K \rightarrow H K$ is the 包含映射 and $\pi: H K \rightarrow H K / H$ is the 商同态。Hence $f$ is a 同态 since it is a 复合映射 of two 同态s, and clearly 核 $\operatorname{Ker} f=\operatorname{Ker} \pi \cap K=H \cap K$。
We will be done if we show that $f$ is 满射,in other words that every 陪集 $x H$,with $x \in H K$,is equal to some 陪集 of the form $k H$ with $k \in K$。But since $x \in H K, x=h k$ for some $h \in H$ and $k \in K$。Since $H$ is 正规的,$h k=k h^{\prime}$ for some $h^{\prime} \in H$,and clearly $k h^{\prime} H=k H$。Thus $x H=h k H=k h^{\prime} H=k H=f(k)$,so that $f$ is 满射。The final equality holds since then
推论 3.2.5. Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $H K=G$ and that $H \cap K=\{1\}$。Then $G / H \cong K$。
证明. By the 定理,$G / H=H K / H \cong K / H \cap K=K /\{1\} \cong K$。
推论 3.2.6. Let $G$ be a 有限群 and $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $H \cap K=\{1\}$ and that $\#(G)=\#(H) \#(K)$。Then $G / H \cong K$。
证明. By the previous 推论,it suffices to show that $H K=G$。We have seen that $\#(H K)=(\#(H) \#(K)) / \#(H \cap K)=\#(H) \#(K)$,since $H \cap K=\{1\}$。Then $H K \leq G$ and $\#(H K)=\#(H) \#(K)=\#(G)$,by our 假设。Thus $H K=G$。
例 3.2.7. Consider the 群 $S_{4}$。We have seen that the 子群
is a 正规子群 of $S_{4}$,with $\#(H)=4$。There is also the (非正规) 子群 $H_{4}$ of $S_{4}$:$H_{4}=\left\{\sigma \in S_{4}: \sigma(4)=4\right\}$。Then $H_{4} \cong S_{3}$ and $\#\left(H_{4}\right)=6$,so that $\#(H) \#\left(H_{4}\right)=24=\#\left(S_{4}\right)$。Finally, by inspection $H \cap H_{4}=\{1\}$。Thus $S_{4} / H \cong S_{3}$。
Here is another 推论 that will come up later:
推论 3.2.8. Let $G$ be a 有限群 with $\#(G)=n m$ and $\operatorname{gcd}(n, m)=1$。Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $\#(H)=n$ and that $\#(K)=m$。Then $G / H \cong K$。
证明. We will show that $H \cap K=\{1\}$ and $H K=G$。By 习题 4.15 (using 拉格朗日定理) $H \cap K=\{1\}$。By 假设 $\#(H) \#(K)=n m=\#(G)$。Thus $G / H \cong K$ by 推论 3.2.6。
24. 单群与有限群的分类
4.1. 小阶有限群. How can we describe all 有限群?Before we address this question, let's write down a list of all the 有限群 of small 阶 $\leq 15$,up to 同构。We have seen almost all of these already。If $G$ is 阿贝尔群,it is easy to write down all possible $G$ of a given 阶,using the 有限阿贝尔群基本定理:$G$ must be 同构 to a 循环群的直积,and any 同构 between two such 直积s is a consequence of the 中国剩余定理。For example, if $\#(G)=n$ and $n$ is a product of 不同素数 then $G$ is 循环的,and hence 同构于 $\mathbb{Z} / n \mathbb{Z}$。The only cases where this doesn't happen for $n \leq 15$ are:
- $n=4$ and $G \cong \mathbb{Z} / 4 \mathbb{Z}$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$。
- $n=8$ and $G \cong \mathbb{Z} / 8 \mathbb{Z}, G \cong(\mathbb{Z} / 4 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$。
- $n=9$ and $G \cong \mathbb{Z} / 9 \mathbb{Z}$ or $G \cong(\mathbb{Z} / 3 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$。
- $n=12$ and $G \cong(\mathbb{Z} / 4 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$。
Note that, for $n=16$,there are already 5 possibilities for $G$。
In case $G$ is not 阿贝尔群,there are many 阶 which can't arise。For example, if $\#(G)=p$,where $p$是素数,then we have seen that $G$是阿贝尔群。We will show soon that, if $\#(G)=p^{2}$,where $p$是素数,then $G$是阿贝尔群。Also, if $\#(G)=p q$,where $p$ and $q$ are distinct 素数,say $p<q$,then $G$是阿贝尔群 unless $q \equiv 1 \bmod p$,and in this case all of the 非阿贝尔群 $G$ of 阶 $p q$ are 同构 and can be described quite explicitly。Thus for example every 阶为15的群都是阿贝尔群,因此是循环群。The only possibilities then for 阶至多为15的非阿贝尔群,up to 同构,are given by:
- $n=6$ and $G \cong S_{3} \cong D_{3}$。
- $n=8; G \cong D_{4}$ or 四元数群 $Q$。
- $n=10$ and $G \cong D_{5}$。
- $n=12; G \cong D_{6}, G \cong A_{4}$, or $G \cong(\mathbb{Z} / 3 \mathbb{Z}) \rtimes(\mathbb{Z} / 4 \mathbb{Z})$,a certain 群 which we shall describe later, time permitting。(Note: $S_{3} \times(\mathbb{Z} / 2 \mathbb{Z})$也是阶为12的非阿贝尔群,but in fact $S_{3} \times(\mathbb{Z} / 2 \mathbb{Z}) \cong D_{6}$。)
- $n=14$ and $G \cong D_{7}$。
Lest one conclude that the list seems manageable, we mention that for $n=16$,there are already 5 非同构阿贝尔群 of 阶 16 as well as 9 非同构非阿贝尔群 of 阶 16,and it is rather complicated to describe them all。Of course, if $\#(G)$ has 阶 17,$G$同构于 $\mathbb{Z} / 17 \mathbb{Z}$且是循环的(particularly 阿贝尔的)。In general, though, if $n$可被素数 $p$的高次幂整除,then it becomes very difficult to list all 群 $G$ with $\#(G)=n$ up to 同构。